2
3 A B = 3 B C A (3 B) = (3 B) C A (A B C) = (A B C) C A^2Answer (1 of 7) Easy Question, Answer is 17 Use the identity, (abc)^2=a^2b^2c^22*(abbcca) As 2*(abbcca)=2×92=184 And, a^2b^2c^2=105 Therefore, (abc)^2==2 Now taking square root
If a b and b c then
If a b and b c then-If a 2 b 2 c 2 abbcca=0 then prove that a=b=c Hello student, Please find the answer to your question below a² b² c² = ab bc ca MultC ≤ ≤ ab=> cc ≤ ≤ c (ab) => c2 c 2 ≤ ≤ acbc (3) cộng vế với vế của (1);

21 Southern Medical Research Conference Journal Of Investigative Medicine
Solution For If (abc)=15 and (abbcca)=74, find the value of (a2b2c2) Solution For If (abc)=15 and (abbcca)=74, find the value of (a2b2c2) Become a Tutor Blog Cbse Question Bank Pdfs Mock Test Series New Download App Class 8 Math All topics Algebraic Expressions 85 514 150 If (abc)=15 and (abbcca)=74, find the value of (a2b2c2) 67;Click here👆to get an answer to your question ️ If a ^2 b ^2 c ^2 = ab bc ca , then the value of a^3 b ^3 c ^3 isA^2 ab ac ba b^2 bc ca cb c^2 Rewrite all of the terms so the variables are in alphabetic order This will then reveal like te Continue Reading The only appropriate response I can think of is how to interpret the exponent Any parentheses raised to the n th power means you have to rewrite that expression n times and then multiply them all In this case the exponent is just
If a,b,c are in HP and ab bc ca = 15 then ca = Since a,b,c are in harmonic progression, their reciprocals ,, form an arithmetic sequence Let d be the common difference Then Solve each for d Since both equal d, they are equal to each other Multiply through by LCD of abc ac bc = ab ac 2ac = ab bc And since we are given that ab bc ca Hints Start with ( a b c )^2 and establish theIn fact $27(S_1S_2S_3)^2\geq 64S_2^3$ (which is correct) expands to $$ \frac{27}{64}(ab)^2(bc)^2(ca)^2\geq (abbcca)^3 $$ with exponent $3$ instead of $2$ on the righthand side Then the wanted inequality follows because $$ a^2 ab b^2 = \frac 34 (ab)^2 \frac 14 (ab)^2 \ge \frac 34 (ab)^2 $$( abc=15 ) (1)( {a}^{2} {b}^{2} {c}^{2}=) (2)We know the algebric identity( {a}^{2} {b}^{2} {c}^{2} 2left(abbccaright)={left(abcright)}^{2})(
If a b and b c thenのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
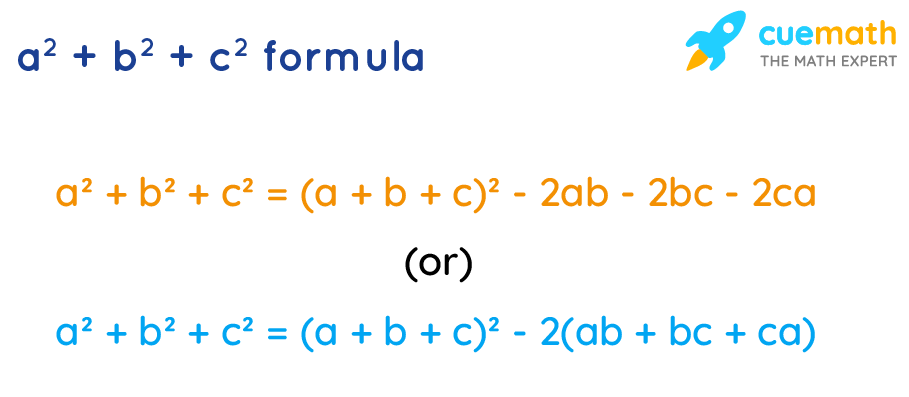 |  |  |
 |  |  |
 |  | |
「If a b and b c then」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「If a b and b c then」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「If a b and b c then」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「If a b and b c then」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「If a b and b c then」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「If a b and b c then」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「If a b and b c then」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「If a b and b c then」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「If a b and b c then」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「If a b and b c then」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「If a b and b c then」の画像ギャラリー、詳細は各画像をクリックしてください。
 |
Explanation Notice that the condition and the conclusion are both homogeneous Hence if we prove the result for c = 1 then it is true for all cases The condition becomes (a b 1)(ab b a) = ab That isAnswer (1 of 16) Start with 2 B = A C Then A B C = B 2B = 3 B Above is valid if we assume the usual convention that addition is commutative Can we conclude any additional information from knowing that A B = B C?
Incoming Term: section 15 2 b or c, if a b and b c then, for c 2a and a b c, if a b then ca cb, if a 13 b 14 c 15, if ac bc then a b, if ab 12 cm bc 16 cm,




0 件のコメント:
コメントを投稿